

Ken Clarkson
AT&T Bell Laboratories
clarkson@bell-labs.com
homepage
I'll talk about computing:
A version of Gram-Schmidt orthogonalization can be used for the
evaluation of various "numerical primitives" needed for these
computations, assuming the input points have integer coordinates less
than about 240. With this assumption, the input data can be in
general (but small!) dimension, and be degenerate, and the code
relatively simple. I'll talk about the specifics of the numerical
primitives, and the applications.
Alpha shapes are useful for finding a surface corresponding to
the "shape" of a set of points; they can be computed using the
Delaunay triangulation.
The basic NN interpolant has a discontinuous gradient at the data sites;
shown here is the interpolant of four sites at the corners of a square with
z>0, plus a site at the center of the square and sites at the boundary of
the domain with z=0.

Alpha shape of a set of atoms in a crystal
Delaunay triangulations have long been used for scattered data interpolation:
given a set of sites (points), and function values at those sites,
find estimates of the function value elsewhere. Here's a piece-wise
linear interpolant for four sites with function values > 0,
and 5 sites with function value = 0:
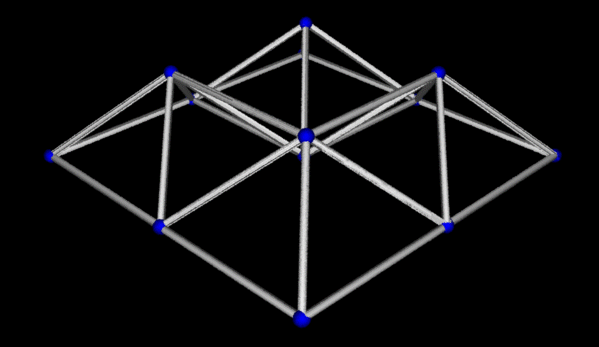
Piecewise-linear interpolant
Natural neighbor interpolation, sometimes called the "area stealing"
approach, is a useful way of interpolating scattered
data that is not as widely available as it might be. I have a code
for NN interpolation for general dimension.

Basic natural neighbor interpolant
There are many ways to make NN interpolants smoother; what is essentially
required is an estimate of the gradient at the data sites. I have
a variant that seems natural, and produces a reasonable interpolant:

A smoother NN interpolant
The program is available ,
except for the natural neighbor interpolation.