Abstract

Previous methods for generating random modal formulae (for the multi-modal logic Km) result either in flawed test sets or formulae that are too hard for current modal decision procedures and, also, unnatural. We present here a new system and generation methodology which results in unflawed test sets and more-natural formulae that are better suited for current decision procedures.

Talk presented at IJCAR-2001, Sienna, Italy, June 2001.

Empirical Testing of Modal Decision Procedures

Why:

to see how a decision procedure performs

How:

try the procedure on lots of formulae

Problem:

generating a reasonable test set

• reasonable difficulty
• good coverage
• no problem formulae

Using Randomly-generated Modal Formulae

Why:

easy to generate lots of formulae

How:

generate formulae according to some recipe, typically

• a conjunction of some number of clauses
• each clause has (usually) three disjuncts
• each disjunct is a (possibly negated) propositional variable or modal formula
• contents of each modal formula is the same as a clause, until a maximum depth is reached

Parameters:

• maximum modal depth (d)
• number of propositional variables (N)
• probability of propositional variables (p)
• number of modal boxes (M; usually 1)
• number of disjuncts in a clause (C; usually 3)
• number of clauses (L; usually varied within each test)

Using Randomly-generated Modal Formulae

Problem:

repeated propositional variables in a clause

• reduce effective size and complexity

Solution:

don't repeat

Problem:

complementary literals in a clause

• in negated modal formulae can make entire formula unsatisfiable

Solution:

don't repeat

Using Randomly-generated Modal Formulae

Problem:

small collection of clauses may be propositionally inconsistent

Solution:

eliminate propositional variables (except at maximum depth)

Problem:

makes the formulae unnatural and very hard

Solution:

new generation methodology

First Change

• restrict variability in number of propositional literals per clause
  • less than one different from pC
  • average number of propositional variables is pC
• eliminates strictly-propositional clauses
• sharply reduces the number of problem formulae

Old Method, Depth 2, Prop. Prob. 0.5

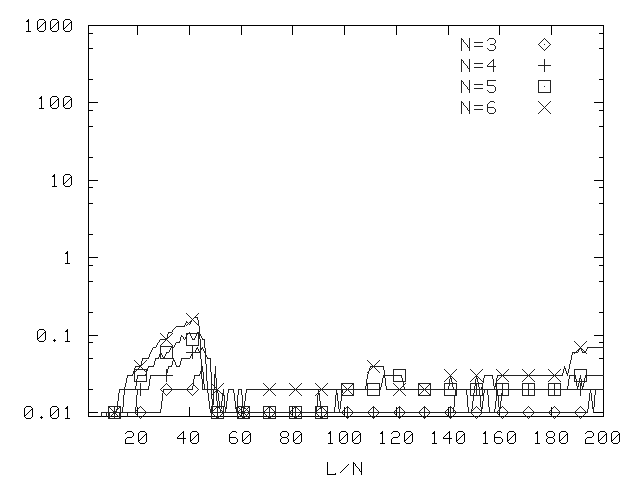
Median difficulty for DLP (version 4.1).

Old Method, Depth 2, Prop. Prob. 0.5

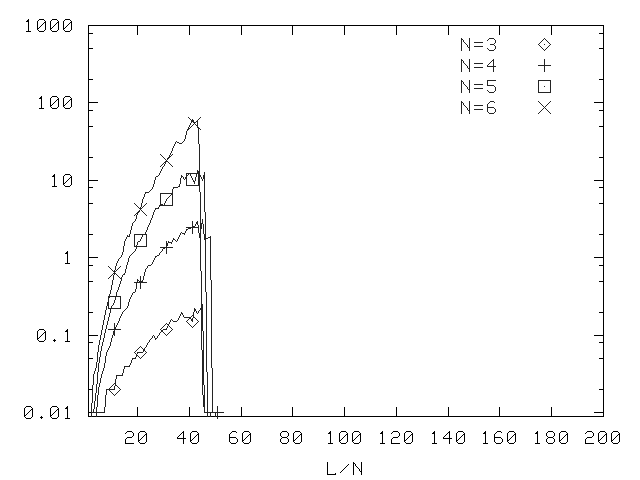
Median difficulty for *SAT (version 1.3).

Old Method, Depth 2, Prop. Prob. 0.5

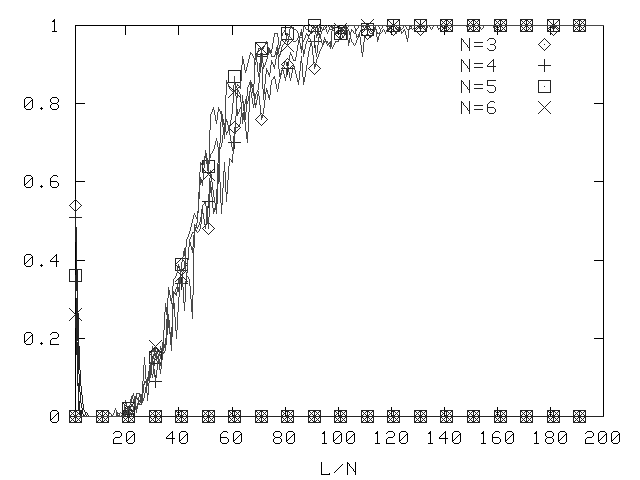
Fraction of formulae that can be determined unsatifiable (or satisfiable) by purely propositional means.

New Method, Depth 2, Prop. Prob. 0.5

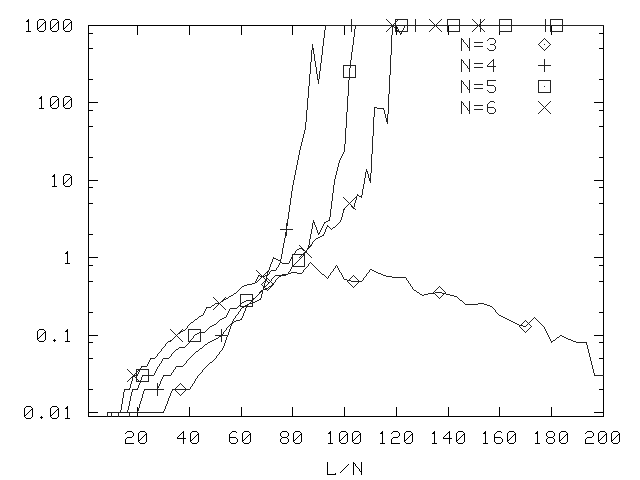
Median difficulty for DLP (version 4.1).

New Method, Depth 2, Prop. Prob. 0.5

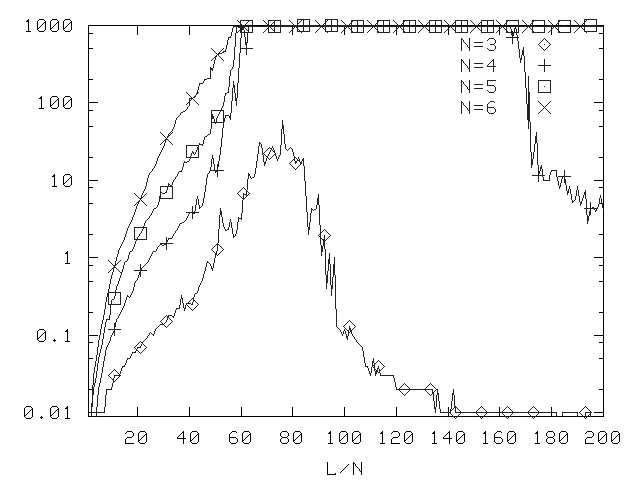
Median difficulty for *SAT (version 1.3).

New Method, Depth 2, Prop. Prob. 0.5

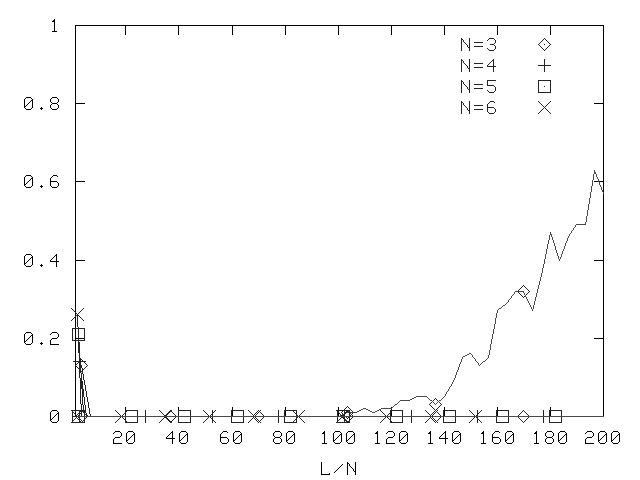
Fraction of formulae that can be determined unsatifiable (or satisfiable) by purely propositional means.

Second Change

• allow the number of disjuncts in a clause to vary
  • manner similar to previous method
• then determine the number of propositional literals in each clause based on the number of disjuncts in that particular clause
• allows for easier test sets
• allows for a new source of variability

New Method, Depth 2, Prop. Prob. 0.5, 2.5 Clauses

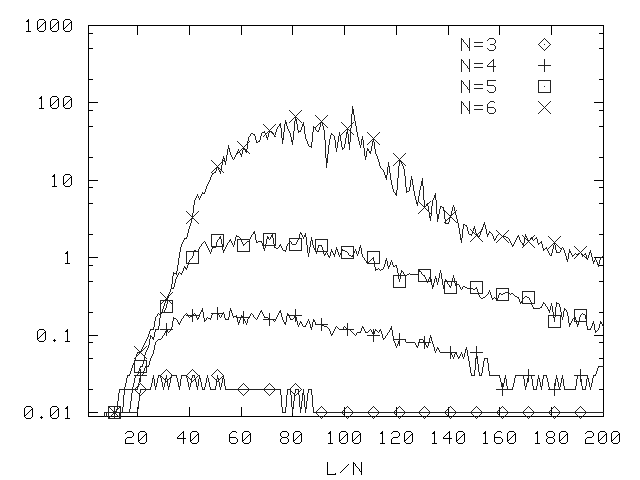
Median difficulty for DLP (version 4.1).

New Method, Depth 2, Prop. Prob. 0.5, 2.5 Clauses

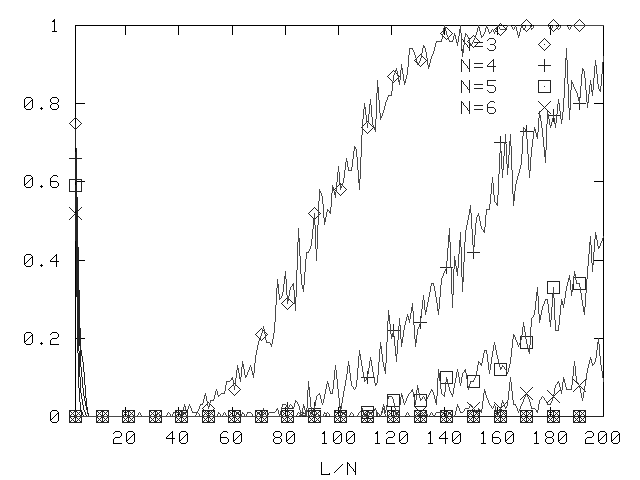
Fraction of formulae that can be determined unsatifiable (or satisfiable) by purely propositional means.

Third Change

• direct specification of probability distributions
  • for the number of disjuncts in a clause
  • for the number of propositional literals in a clause
  • can depend on modal depth and on number of disjuncts in the clause
• example with
  • m=1
  • C=[[1,8,1]]
  • p=[[[1,0],[0,3,0],[0,3,3,0]]]
  • N=3,4; d=3,4

C=[[1,8,1]]; p=[[[1,0],[0,3,0],[0,3,3,0]]]; N=3,4; d=3,4

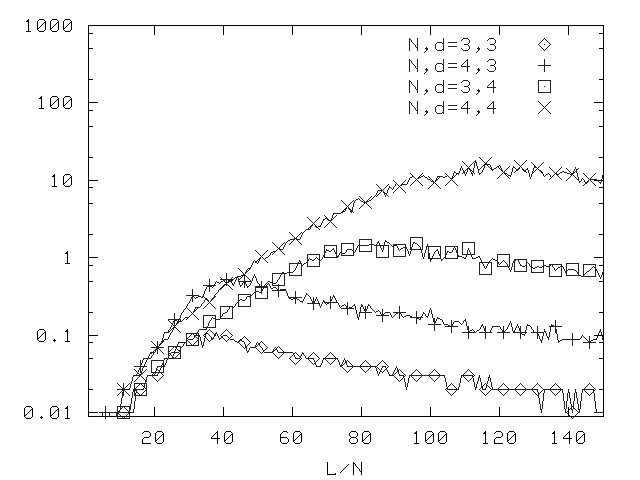
Median difficulty for DLP (version 4.1).

C=[[1,8,1]]; p=[[[1,0],[0,3,0],[0,3,3,0]]]; N=3,4; d=3,4

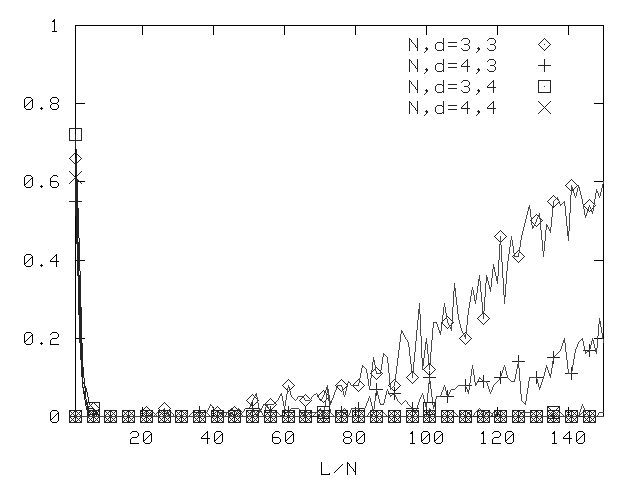
Fraction of formulae that can be determined unsatifiable (or satisfiable) by purely propositional means.

Summary

• New generator for random modal formulae
• Benefits
  • no ``errors'' in formulae
  • can generate test sets with fewer problem formulae
  • can generate reasonable test sets with deeper modal depth
• Drawback
  • more parameters, so harder to exhaustively explore parameter space
• Available at http://ect.bell-labs.com/who/pfps/dlp